体重はカロリーだ！

前回の、

消費カロリー　－　摂取カロリー　＝　体重減少

という式を、

消費カロリーを増やせば体重が減るし、
摂取エネルギーを減らしても体重が減る、
だから、（単純に、また、やみくもに）運動して食事を減らすと体重が減る、
と捉えている人がいます。

これは、式に出てくる「体重減少」の答えとして、
体重が「増える」、「減る」、という２つの値しか想定していません。
本来この式から得られる情報が活用できていない、もったいない解釈です。

この式は、単純に増えるか減るかだけでなく、活用すると、
どれくらい運動したら、また、食事の量をどれくらい減らしたら、
体重がどれだけ減るか、ということを、
具体的・量的に（精密に）教えてくれる使い出のある式なのです。

（ためしてガッテンというテレビ番組の「計るだけダイエット」で失敗している人が多いのは、方法そのものが、体重が増えるか減るかの２方向で考えるだけで、量的な検討をしていないからです）

例として、体重75kgの人が30分歩いた時に使うカロリーは140kcalです。
これは、体脂肪（正しくは脂肪組織の重量）に換算すると、
1gの体脂肪には7kcal（7.2kcalという場合もあります）のカロリーが
蓄えられるので、（140÷7≒）20gに相当します。

そのあとアイスクリームを１カップ（320kcal）食べると、
体脂肪は（320÷7≒）46g増えてしまうので、
体脂肪は差し引き（46－20≒）26g増えてしまいます。
かりに、歩いて食べた後に、汗などで体重がどれだけ減っていても、
体脂肪は増えているので、続けていると反って体重が増えることになります。
（これが「計るだけダイエット」失敗の原因です）

このように、量的（数値的）な検討をせずに、
「運動すれば体重が減るはず」と思ってやみくもに実行しても、
期待していた効果は得られません。

このブログで何度も述べているように、
運動で消費するカロリーは多くないので、
食事のカロリーを（楽な方法で）減らすことに集中した方が
確実な減量効果が得られます。

このように、単純に増えるか減るかだけでなく、
量的に検討することによって、運動や食事の行動が、
体重をどう変化させるが、より具体的に分かります。
これを、精密さが増えることで、その分、失敗が減る、ということができるでしょう。

精密さは、使う場面によって、必要な度合いが違います。

たとえば、短期的な（日数の単位での）行動では、
7kcal≒体脂肪1gという精密さで十分ですが、
中長期的に（月・年単位で）考えるときには、
精密さの度合いを高めて計算しなければなりません。

１日に240kcal減らして30日たつと、
240×30＝72000kcal。これは、72000÷7≒1000g＝1kg。
すなわち、体重が１ヵ月で1kg減ることになります。
この辺りではあまり大きな誤差は生じません。

ところが、３ヵ月で3kg、すなわち１ヵ月当たりで1kgは減りませんし、
６ヵ月なら、1ヵ月当たりの体重変化はもっと少なくなります。
なぜなら、体重が減ってくると、消費カロリーが減る
（消費カロリーは体重に比例する）からです。

これを組み入れて計算するのは、
高校で習う数学の範囲を超えていますが、
理系の大学出身者なら別に難しいことではありません。
（医学部は理系ですが、他の学部のようには数学を使わないので、
始めて計算するときには少し骨が折れました）

計算式に興味がある人は「メタボ氏のための体重方程式p198-199」
を見てもらうとして、

　　【図をクリックすると体重方程式のページが開きます】

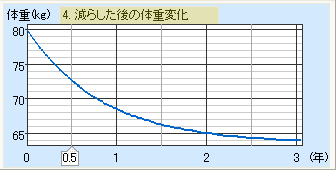
そうでない人は、その式で計算した体重のグラフを見てください。
このグラフを見ると、月単位になると、だんだん体重が減りにくくなる様子がよく分かります。

ですから、
「1日当たり○○カロリーでも、1年続けると△△kg減る」や、
「△△kgを、□ヵ月で減らすためには、１日当たり○○カロリー減らす」
と書いてあっても、実際に体重がそれだけ減ることはないので、誤りです。
どちらも、体重が減ると消費カロリーが減ることを、
（文字通り）計算に入れていないからです。

科学では、小さいことを無視して、物事を単純化して考える、
というのが基本的な方法になっています。しかし、単純化しすぎると、
現実に起こっている現象が説明できなくなりますから、
必要に応じて精密化・複雑化していく必要があります。

従来使われていた、7kcal＝体重1gという式に、
消費カロリーは体重に比例する、ということを組み入れて、
月単位の体重変化を説明する、というのは、精密化・複雑化する例です。

そして、わずかな精密化・複雑化によって、
摂取カロリーを減らしたり消費カロリーを増やしたりしたときに
体重が減りにくくなる、という現象を説明できます。

これによって、「停滞期」や「ホメオスタシス」や「体重のセットポイント」などという
神秘的であいまいな概念を使う必要はなくなりました。